CSE 212 | Learning Activities

Learning Activity: Trees

Trees are like linked lists in that nodes are connected together by pointers. However, unlike linked lists, the nodes in a tree can connect to multiple different nodes. We will look at the following types of trees: binary trees, binary search trees, and balanced binary search trees.

Binary Trees

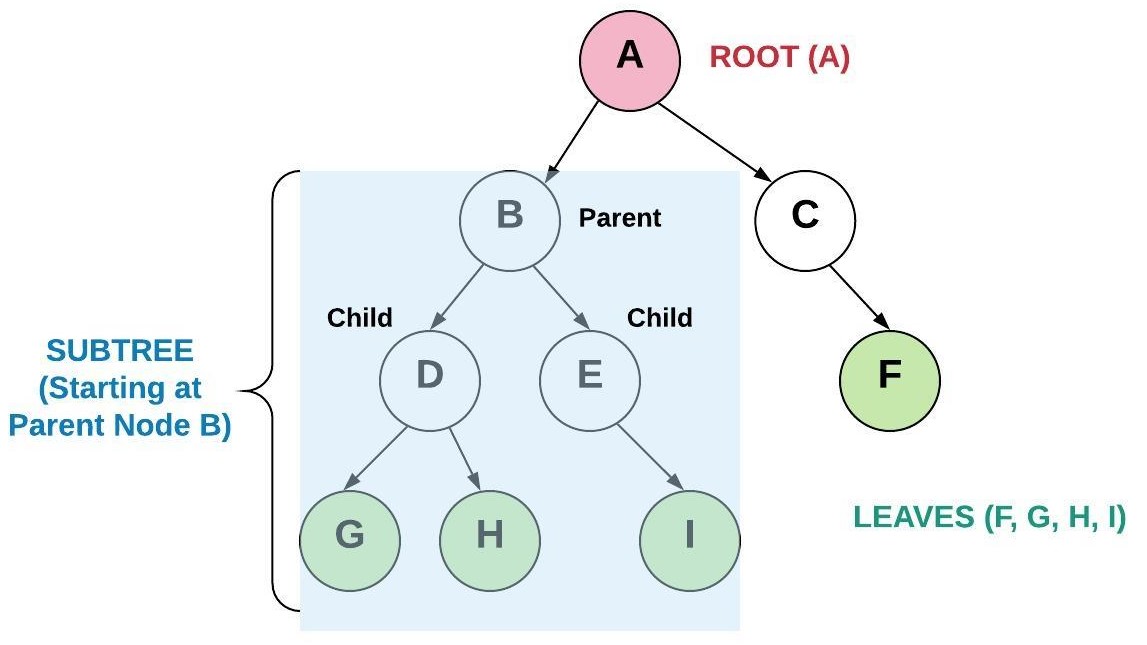
A binary tree is a tree where each node links to no more than two other nodes. In the picture below, the top node is called the root node. The nodes that connect to no other nodes are called leaf nodes. A node that has connected nodes is called a parent node. The node connected to the parent are called child nodes. The nodes to the left and right of any parent node form a subtree. There is always only one root node. While not shown in the picture, it is common for child nodes to also point back up to the parent node (similar to a linked list).

Shows a Binary Tree where the top (node A) is called the root, the nodes that do not connect to any other nodes are called leaves (node F, G, H and I). Node A connects to nodes B and C. Node B connects to node D and E. Node C connects only to node F. Node D connects to nodes G and H. Node E connects to Node I. A subtree is formed from a any parent node such as parent node B and includes all of the children nodes D, E, G, H, and I. — Binary Tree

Binary Search Trees

A binary search tree (BST) is a binary tree that follows rules for data that is put into the tree. Data is placed into the BST by comparing the data with the value in the parent node. If the data being added is less than the parent node, then it is put in the left subtree. If the data being added is greater than the parent node, then it is put in the right subtree. If duplicates are allowed than the duplicate can be put either to the left or to the right of the root. By using this process, the data is stored in the tree sorted.

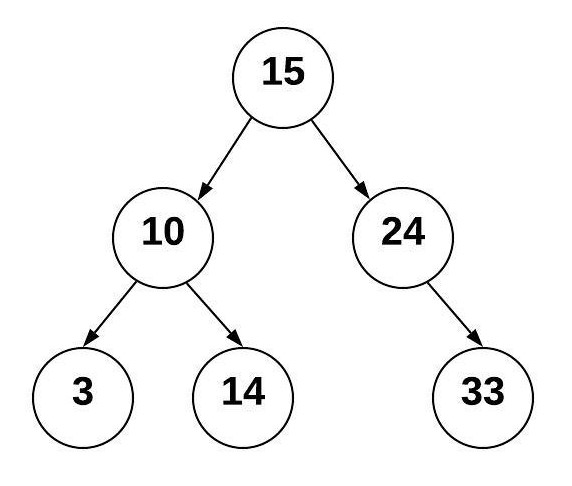
Shows a Binary Search Tree where the root node is 15. The 15 is connected to 10 (on the left) and 24 (on the right). The 10 is connected to 3 (on the left) and 14 (on the right). The 24 is connected to 33 (on the right). — Binary Search Tree

Using the tree above, we can determine where to put additional items. We always start at the root node and compare the new value with it. We keep comparing until we have found an empty place for the new node. For example, to insert the value 20, do the following:

Start at the root node 15 and compare with the new value 20
Since 20 is greater than 15, goto the right and visit node 24
Since 20 is less than 24, goto the left and see there is no additional node
Insert 20 in the empty spot to the left of 24

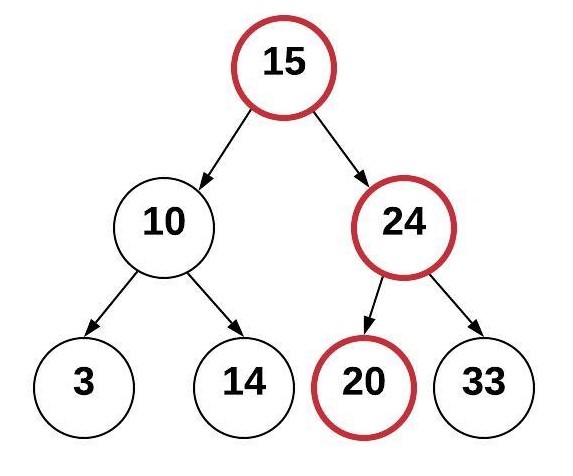
Shows the same binary search tree with node 20 added to the left of node 24. Nodes 15, 24, and 20 are highlighted to show the path to find where the new node was inserted. — Add Node to BST

The process that we used to find where to put the new node was efficient. The process that we used to actually insert the node at that position was efficient. If we had a dynamic array containing sorted values, we would have a O(log n) operation to find where to insert the new value and a O(n) operation to actually insert it at that position. If we had a linked-list containing sorted values, we would have a O(n) operation as we search for the proper location to insert a value into the proper sorted position, then a O(1) operation to actually insert the node. By using the BST, we are able to exclude a subtree with each comparison. This ability to split the job in half recursively results in O(log n). Maintaining sorted data in a BST performs better than other data structures.

However, the only reason we had O(log n) in the example above was because the tree was "balanced". To see the difference between a balanced and an unbalanced tree, we will construct a tree with the same values but in a different order. The reason why the previous tree has 15 as the root node is because 15 was added first. This time, we will add the values in the following order: 3, 10, 14, 15, 20, 24, 33 (purposefully in ascending order).

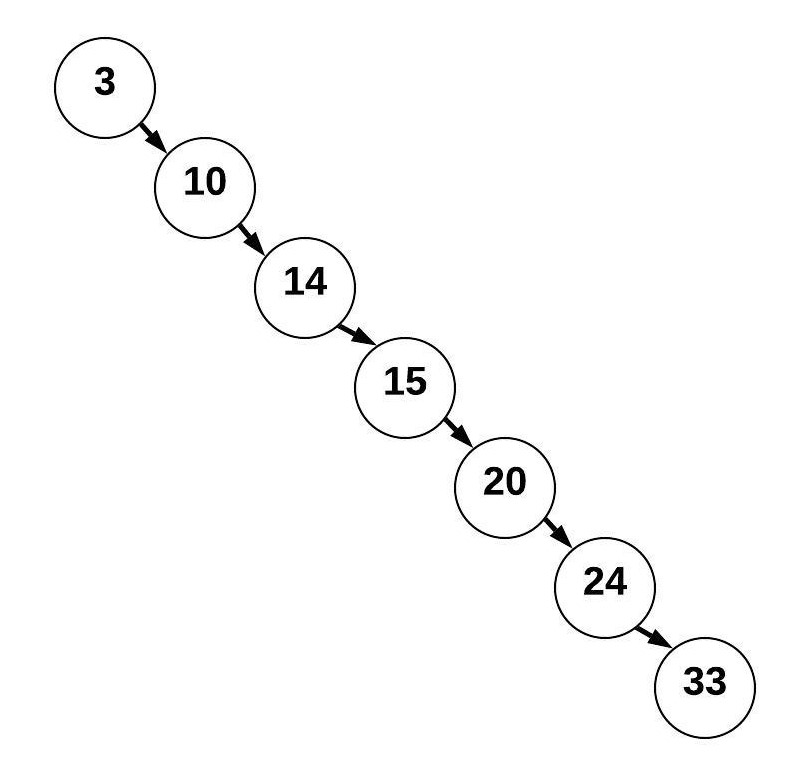
Shows a binary search tree with a root node of 3. Each subsequent node is attached to the right including 10, 14, 15, 20, 24, and 33. — Unbalanced BST

This tree is a BST but looks more like a linked list. This BST is unbalanced has a resulting performance for searching of O(n) instead of O(log n).

Balanced Binary Search Trees

A balanced binary search tree (balanced BST) is a BST such that the difference of height between any two subtrees is not dramatically different. The height of a tree can be found by counting the maximum number of nodes between root and the leaves. Since it is not reasonable to expect that the order of data will result in a balanced BST, numerous algorithms have been written to detect if a tree is unbalanced and to correct the unbalance. Common algorithms include red black trees and AVL (Adelson-Velskii and Landis) trees. The example below shows an AVL tree which is balanced because the difference of height between subtrees is less than 2.

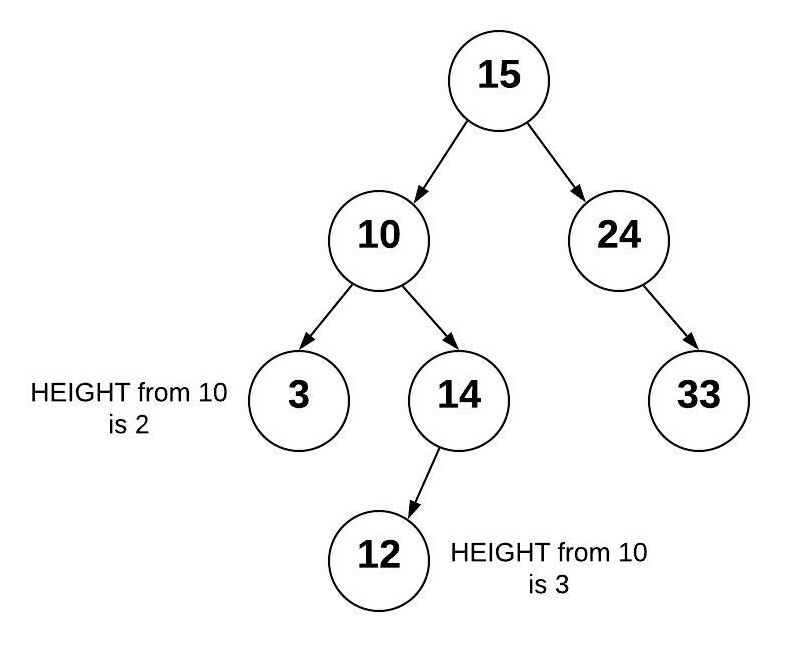
Shows an AVL tree where the root node is 15. The 15 is connected to 10 (on the left) and 24 (on the right). The 10 is connected to 3 (on the left) and 14 (on the right). The 12 is connected to 14 (on the left). The 24 is connected to 33 (on the right). Looking at the subtree starting with 10, the height to the 3 on the left is 2. The height of the subtree to the 12 on the right is 3. — Balanced AVL Tree`

If we add 13 to the right of the 12, we end up with an unbalanced AVL tree because the height of the right subtree from 10 is now 2 more than the left subtree.

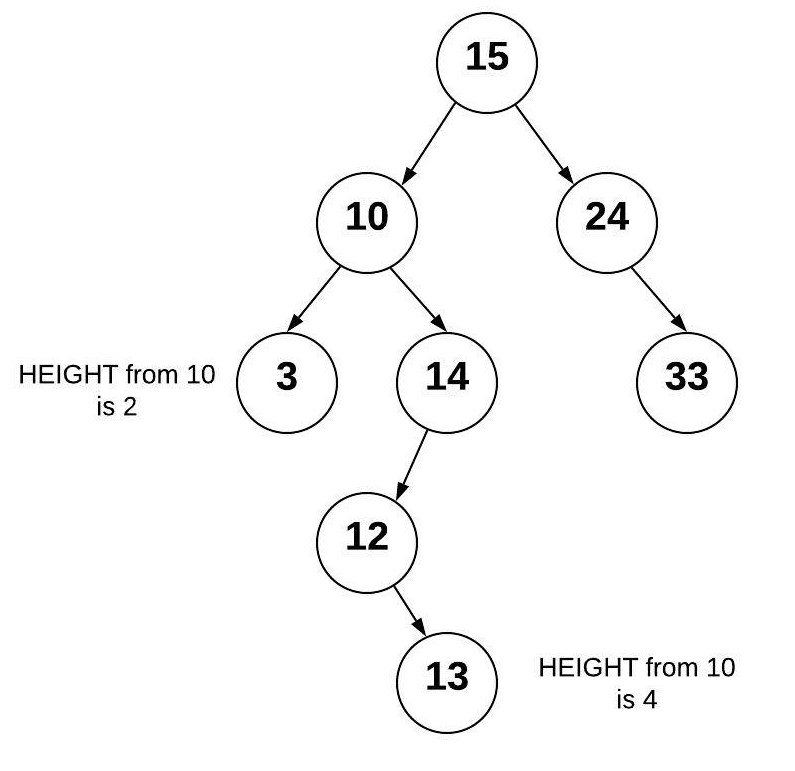
Shows the same AVL tree but with node 13 added to the right of 12. The height between node 10 and node 13 is now 4. — Unbalanced AVL Tree after Adding Node

The AVL algorithm will detect that the tree has become unbalanced. To balance the tree, a node rotation will be performed. For our tree, we can rotate the node with 13 so that nodes 12 and 14 are children nodes of the 13. When this rotation is done, the tree returns to a balanced state. An AVL tree will always be a Balanced BST and therefore benefit from O(log n) performance.

Shows the same AVL tree balanced again by moving the 13 to be the node of the subtree with 12 and 14 as children. — Rebalanced AVL Tree

BST Operations

BST operations can be very complicated (balanced BST's offering even more complication). We will look at two operations in our study of trees: inserting and traversing.

Inserting into a BST

Inserting into a BST is a recursive operations:

Smaller problem: Insert a value into either the left subtree or the right subtree based on the value.
Base case: If there is space to add the node (the subtree is empty), then the correct place has been found and the item can be inserted.

The code for inserting into a BST is shown below. Some things to note are as follows:

A node is defined as an object (in this example) of class Node. This is similar to what we saw with the linked list class. The Node class contains three things: Data (the value), Left (pointer to the left node), and Right (pointer to the right node).
There are two Insert functions:
- The first BinarySearchTree.Insert function is the one called by the user who wants to insert a value into the tree. This function is used to call the recursive function Node.Insert on the root node. As a special case, if the root node is empty (null), then we will put the new Node in the root without using any recursion.
- The second Node.Insert calls itself until it finds a empty position in which to insert the value.
We will follow a similar pattern for many of the recursive functions we write for the BinarySearchTree.
In the Node.Insert function, we should identify the base case and the recursive calls to the correct subtrees.


public class BinarySearchTree : IEnumerable<int>
{
    private Node? _root;

    // Insert 'value' into the BST.  If the BST is empty, then
    // set the root equal to the new node. Otherwise, use
    // Node.Insert to recursively find the location to insert.
    public void Insert(int value)
    {
        if (_root is null)
            _root = new Node(value);
        else
            _root.Insert(value); // Start inserting at the root
    }
}

public class Node
{
    // This function will look for a place to insert a node
    // with 'value' inside of it. The current subtree is
    // represented by this instance of Node. This function
    // is intended to be called the first time by the
    // BinarySearchTree.Insert function.
    public void Insert(int value)
    {
        if (value < Data)
        {
            // The value belongs on the left side
            if (Left is null)
            {
                // We found an empty spot
                Left = new Node(value);
            }
            else
            {
                // Need to keep looking; Call Insert
                // recursive on the left subtree
                Left.Insert(value);
            }
        }
        else
        {
            // The value belongs on the right side
            if (Right is null)
            {
                // We found an empty spot
                Right = new Node(value);
            }
            else
            {
                // Need to keep looking; Call Insert
                // recursive on the right subtree
                Right.Insert(value);
            }
        }
    }
}

Traversing a BST

We traverse a BST when we want to display all the data in the tree. An in-order traversal will visit each node from smallest to largest. A similar process can be followed to visit each node from the largest to the smallest. This is also a recursive process:

Smaller problem: Traverse the left subtree of a node, use the current node, and then traverse the right subtree of the node.
Base case: If the subtree is empty, then don't recursively traverse or use anything.

The code for traversing a BST is shown below. In addition to understanding that there are two calls - one to start the recursion, and another to keep it going, here are some insights about creating iterators (IEnumerable) in C#:

There is an interface IEnumerable<int> which C# uses to enable foreach loops over custom classes. In order to implement the IEnumerable<int> interface, the class must implement 2 GetEnumerator functions.
- The first IEnumerator IEnumerable.GetEnumerator() is the required function for all IEnumerable objects, but it doesn't specify the type of item being enumerated.
- The second public IEnumerator<int> GetEnumerator() is what is called when using a foreach loop to inform the compiler that each loop will produce an int value.
```
var bst = new BinarySearchTree();

foreach (var intValue in bst)
{
    Console.WriteLine(intValue);
}
```
The IEnumerator return type is generated using the yield return syntax. Whenever you use yield return, the function will always return an IEnumerator with the values of each time yield return is called. There is no way to call yield return recursively, so our implementation is to gather all values into a List using recursion, and then use yield return for all values in the List.


public class BinarySearchTree : IEnumerable<int>
{
    private Node? _root;

    // Yields all values in the tree
    IEnumerator IEnumerable.GetEnumerator()
    {
        // call the typed version of the method
        return GetEnumerator();
    }

    // Iterate forward through the BST
    public IEnumerator GetEnumerator()
    {
        var numbers = new List();
        TraverseForward(_root, numbers);
        foreach (var number in numbers)
        {
            yield return number;
        }
    }

    private void TraverseForward(Node? node, List values)
    {
        if (node is not null)
        {
            TraverseForward(node.Left, values);
            values.Add(node.Data);
            TraverseForward(node.Right, values);
      }
   }
}

BST in C#

In your assignment this week you will be writing your own BST class. C# does has a built-in tree called a SortedSet<T> which is an implementation of a Red Black Tree. The table below shows the common functions in a BST.

Common BST Operation	Description	Performance
insert(value)	Insert a value into the tree.	O(log n) - Recursively search the subtrees to find the next available spot
remove(value)	Remove a value from the tree.	O(log n) - Recursively search the subtrees to find the value and then remove it. This will require some cleanup of the adjacent nodes.
contains(value)	Determine if a value is in the tree.	O(log n) - Recursively search the subtrees to find the value.
traverse_forward	Visit all objects from smallest to largest.	O(n) - Recursively traverse the left subtree and then the right subtree.
traverse_reverse	Visit all objects from largest to smallest.	O(n) - Recursively traverse the right subtree and then the left subtree.
height(node)	Determine the height of a node. If the height of the tree is needed, the root node is provided.	O(n) - Recursively find the height of the left and right subtrees and then return the maximum height (plus one to account for the root).
size()	Return the size of the BST.	O(1) - The size is maintained within the BST class.
empty()	Returns true if the root node is empty. This can also be done by checking the size for 0.	O(1) - The comparison of the root node or the size.

Video Discussion (Optional)

The following video is optional. It presents a brief discussion of the topic.

Activity Instructions

Complete the following activity:

Activity: Tree Traversal Practice

There are three types of traversals that can be performed: pre-order, in-order, and post-order.

The pre-order traversal visits the current node first, then visits the left subtree and then the right subtree.
The in-order traversal traverses the left subtree first, then visits the current node, then traverses the right subtree.
The post-order traversal visits the left and right subtrees first and then visits the current node.

Practice doing all three types of traversal on the following tree. Use a pencil and paper to write down the order of the nodes that will be visited. What do you notice about the order of the in-order traversal numbers?

Solution (Click to Expand)

Pre-order: 15, 10, 3, 14, 24, 33
In-order: 3, 10, 14, 15, 24, 33
Post-order: 3, 14, 10, 33, 24, 15

The order of the nodes in the in-order traversal is done in a proper numerical order.

Key Terms

AVL Tree: Adelson-Velskii and Landis Tree. A balanced binary search tree that is checked unbalanced height after every modification to the tree. If the tree is unbalanced, then pre-determined algorithms are used to balance the tree.
balanced: A tree is balanced if the the height of the tree from the root to each leaf is consistent for all subtrees. The measure of consistentency will vary between algorithms but usually does not exceed a height difference of 1.
balanced binary search tree: A binary search tree which is balanced or restructured to be balanced. A balanced binary search tree has O(log n) performance when searching.
binary search tree: A binary tree that puts data less than the root to the left and greater than the root to the right. This type of a tree enables searching algorithms to be efficient.
binary tree: A tree that has up to two children for each node.
child: A child is a node connected from a parent node.
leaf: A leaf is a node that has no children.
node: An entry in a tree that contains both the value and pointers to any children nodes.
parent: A parent is a node that connects to children nodes.
Red Black Tree: A self-balancing binary search tree.
root: The first parent in a tree.
subtree: Subset of a tree made by selecting a node to be the root and including all the children from that node.
traverse: The process of visiting all nodes (and subsequently their values) in a tree. Used frequently with a binary search tree using recursion to start at the leaf node that contains the smallest value and going to the leaf node that contains the largest value.
trees: A data structure that starts with a root node and is subsequently connected to multiple nodes according to a relationship between the nodes. The tree does not have any circular loops or unconnected nodes.

Submission

When you have finished this learning activity, return to I-Learn and submit the associated quiz there.