CSE 212: Programming with Data Structures

W05 Code: Recursion

Instructions

This assignment must be completed individually to ensure you are meeting all course outcomes. You should not complete this assignment within a group. If you obtain help from a tutor, the tutor should help you understand principles but should not help you answer these problems. It is an honor code violation to obtain answers for these problems from others including using the internet (i.e. sites that allow students to share their solutions).

Running and Debugging

As you solve the problems, remember to use the principles learned so far in the course:

All of the files for this assignment will be found in the week05/code folder in the course repository. You will commit changes to your own repository for your submission for this assignment.

Problem 1: Recursive Squares Sum

Implement the SumSquaresRecursive function to find the sum 1^2 + 2^2 + 3^2 + ... + n^2 using recursion. Remember to both express the solution in terms of recursive call on a smaller problem and to identify a base case (terminating case). If the value of n <= 0, just return 0. A loop should not be used.

Problem 2: Permutations Choose

Using recursion return permutations of length size from a list of letters. This function should assume that each letter is unique (i.e. the function does not need to find unique permutations). In mathematics, we can calculate the number of permutations using the formula:

letters.Length! / (letters.Length - size)!

For example, if letters was new[]{'A','B','C'} and size was 2 then the following would be returned in the results array: AB, AC, BA, BC, CA, CB (might be in a different order). You can assume that the size specified is always valid (between 1 and the length of the letters list).

Problem 3: Climbing Stairs

Imagine that there was a staircase with s stairs. We want to count how many ways there are to climb the stairs. If the person could only climb one stair at a time, then the total would be just one. However, if the person could choose to climb either one, two, or three stairs at a time (in any order), then the total possibilities become much more complicated. If there were just three stairs, the possible ways to climb would be four as follows:

With just one step to go, the ways to get to the top of s stairs is to either:

We don't need to think about scenarios like taking two single steps from the third to last step because this is already part of the first scenario (taking a single step from the second to last step).

These final leaps give us a sum:

CountWaysToClimb(s) = CountWaysToClimb(s-1) + CountWaysToClimb(s-2) + CountWaysToClimb(s-3)

To run this function for larger values of s, you will need to update this function to use memoization. The parameter remember has already been added as an input parameter to the function for you to complete this task.

Problem 4: Wildcard Binary Patterns

A binary string is a string consisting of just 1's and 0's. For example, 1010111 is a binary string. If we introduce a wildcard symbol * into the string, we can say that this is now a pattern for multiple binary strings. For example, 101*1 could be used to represent 10101 and 10111. A pattern can have more than one * wildcard. For example, 1**1 would result in 4 different binary strings: 1001, 1011, 1101, and 1111.

Using recursion, insert all possible binary strings for a given pattern into the results list. You might find some of the string functions like IndexOf and myStr[..X] or myStr[X..] (string indexing) to be useful in solving this problem.

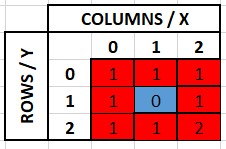
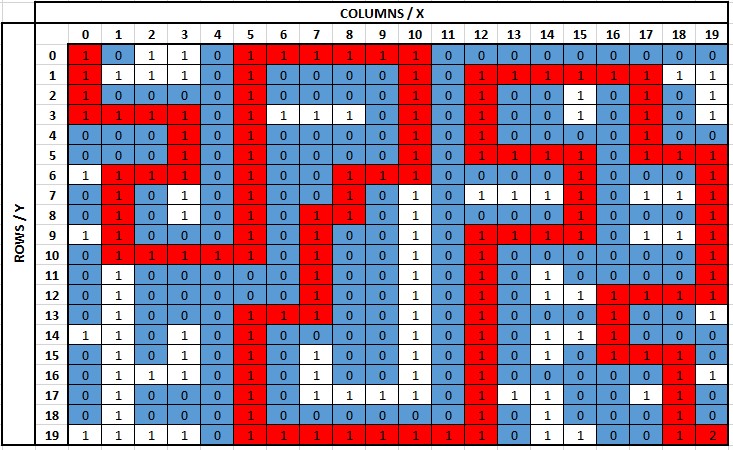
Problem 5: Maze

A maze is defined as an array of integer values. The array is defined for an n x n maze, the first n elements of the array represents the first row in the maze. The next n elements define the 2nd row and so on. You can assume that the maze will be square (same number of rows and columns). The values of the array define each maze position as:

In the code, there are two sample mazes. Each maze shows 0, 1, or 2 in each box. The blue boxes are walls and the white boxes are path ways. The solution to each maze is highlighted in red. Note that the small maze has two possible solutions and the big maze has only one possible solution.

Shows a 3 by 3 maze (indices 0 to 2) populated as described in the code for the small_maze test. The expected output shown in the code for this maze is highlighted in the picture.
Small Maze Example
Shows a 20 by 20 maze (indices 0 to 19) populated as described in the code for the small_maze test. The expected output shown in the code for this maze is highlighted in the picture.
Big Maze Example

The IsEnd and the IsValidMove functions are already written for you. These functions assume that the first square in the maze is (0,0). These functions also assume that you can't leave the boundaries of the maze and that you can't visit the same square in the same path (no circles). The IsEnd will return true if the x and y coordinate represent the end of the maze. The IsValidMove will return true if the movement to x and y is within the maze boundaries, does not represent a wall, and is not someplace we have already been.

The currPath variable is a list of (x,y) tuples that represent the path we are currently on. If you add a new position to the path, make sure that you add the tuple to the list so that the IsValidMove function works properly.

The goal is to implement the SolveMaze function to insert all paths to the end square into the results list using recursion. When you find a path, then adding it to the list of results will be as simple as results.Add(currPath.AsString()).

Grading

To receive full credit on this assignment, you must successfully complete any four of the five problems. If you complete all five problems you are eligible to receive extra credit.

Submission

When you have finished the assignment:

  1. Make sure that all of your changes are committed to your course repository.
  2. Push your latest changes to GitHub.
  3. Return to I-Learn to submit a link to your GitHub repository.

Other Links: