W03 Learning Activity: Sets
Overview
Previously we learned about lists, stacks, and queues. The position of each item in these data structures was very important to the proper use of the data structure. Not all data structures worry about the order of the data. The set data structure is an example of one for which order is not important.
Characteristics of Sets
Besides the lack of order, the set has another difference. Could we add duplicate data to a list, stack, or queue? The answer is yes, and this situation is very common. However, the set is constrained to not allow duplicates. Knowing that there will be no duplicates (and because we don't care about the order) allows us to store the information in a set to make it very efficient to determine if data is in the set. This test of membership in the set is the most important operation belonging to this data structure. Using a technique called hashing, the set is able to add, remove, and test for membership in O(1) time.
Hashing and Sets
To achieve the O(1) time for set operations, we will consider a very simple example. Assume we wanted to store
all positive one digit numbers (0 to 9) into an array. How would we store these numbers if we wanted to have an
O(1) performance for adding, removing, or testing for membership? If we used the value to determine the index into
the array, we might be able to achieve O(1). Consider the function index(n) = n. If we wanted to add the number 7, then we
would use this simple function to determine the index to put the number 7 is index 7. If we wanted to add the
number 4, then we would put it into our function and get the index 4. For this to work, our array will need to be
exactly size 10.
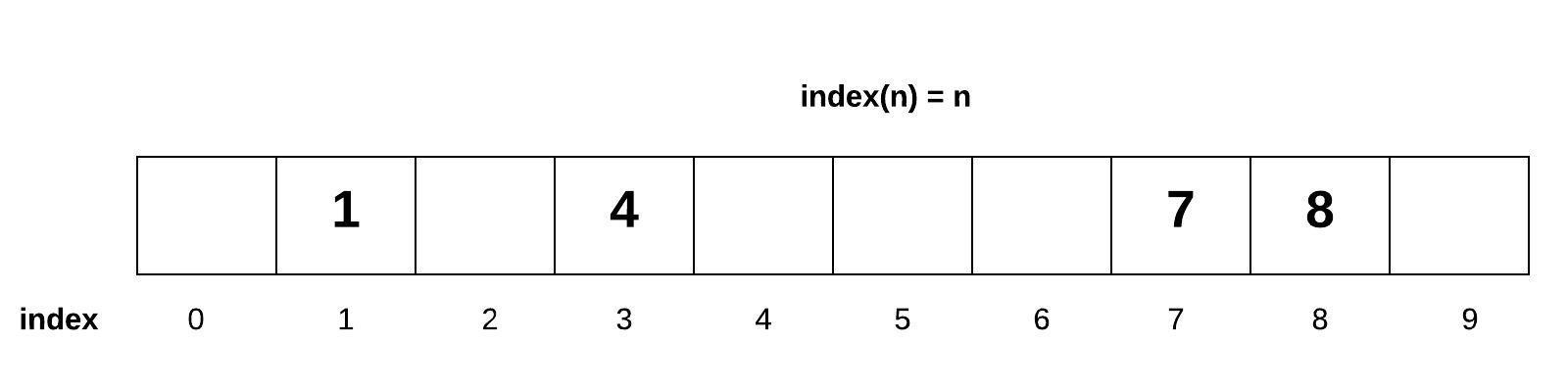
The array above shows several one digit numbers added to our array according to the rule index(n) = n. Notice that if we wanted to know if a number
existed in the array, then we would use the formula to lookup the index. This would result in an O(1) performance.
Also notice that the array is not populated in the same way that we learned about dynamic arrays. We call this a
sparse array because the array is not guaranteed to be filled from left to right.
We call this sparse array a set. Notice that there is only one place for each value to go. Therefore, the set does not allow duplicates because there would be no place for the duplicate value to be placed.
Imagine we changed this simple example to include all nine digit positive numbers (0 to 999,999,999). How big
would the array need to be store these numbers and still achieve O(1) performance? We would need an array size of
1 billion. While this would work, the amount of memory is prohibitive. To store just one 10 digit number, we would
need memory for a 1 billion sized spare array. Could we do this with something smaller such as a sparse array size
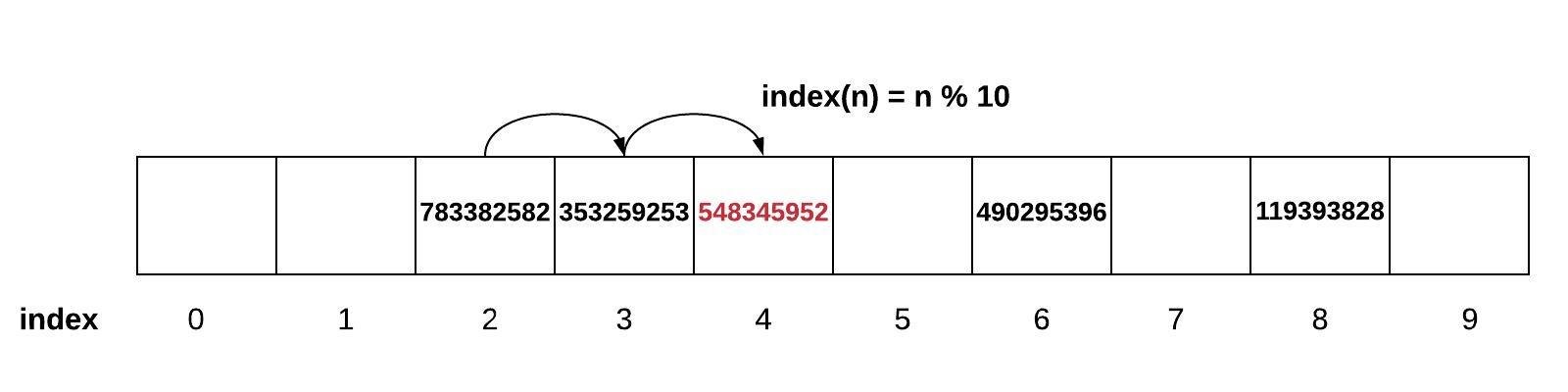
of 10? We can accomplish this by using the modulo (%) operator. If we wrote the equation as index(n) = n % 10, then we would be able to store values
properly. The value 353,259,253 would be placed based on index(353,259,253) = 353,259,253 % 10 = 3. The value
783,382,582 would be placed in index 2.

Our formula for calculating the index for an integer can be generalized to index(n) = n % sparseArraySize. This works great for
numbers; however, if we wanted to store more than just integers into our set, we would need to turn our data into
an an integer value before determining the index. The formula would look like index(data) = hash(data) % sparseArraySize, where hash is a hashing function. The hashing
function calculates an integer value based on the data. Because hashing is integral to using sets, C# has a method
defined for every data type called GetHashCode(). The
values returned by this hashing functions may vary each time the program is run, but it will be consistent during
the run.
| Data Type | C# Code | Hash Code |
|---|---|---|
| positive int | 3.GetHashCode() |
3 |
| negative int | -3.GetHashCode() |
-3 |
| string | "cat".GetHashCode() |
-1599535192 |
| other string | "dog".GetHashCode() |
-73217838 |
| float/double | 3.14.GetHashCode() |
300063655 |
| bool | true.GetHashCode() |
1 |
| List/object | new List<string>().GetHashCode() |
27252167 |
If we only have 100 spots and there are up to 10 billion possible values, it's reasonable to expect that perhaps there is a weakness in the data structure. Using the same diagram above, what would happen if we tried to add 548,345,952? This would also be placed in index 2. This is called a conflict.
Dealing with Conflicts
There are two common ways to deal with conflict in a sparse array. The first option is called open
addressing. If we use our index(n) hashing
function and find that something already occupies the space (or the item in that space is not what we are looking
for), then open addressing strategy will tell us move to the next available space. There are multiple ways that
this can be done, but the simplest method would be to look to the right one spot at a time. The danger with this
approach is that a conflict can result in the creation of more conflicts. In the example below, when 548,345,952
was added, since there was a conflict in index 2, we would move over to index 3. Since there is something in index
3 already, we have to move to index 4. Unfortunately, now any number ending in a 4 will also find a conflict. This
can result in rapidly growing clusters of conflicts.
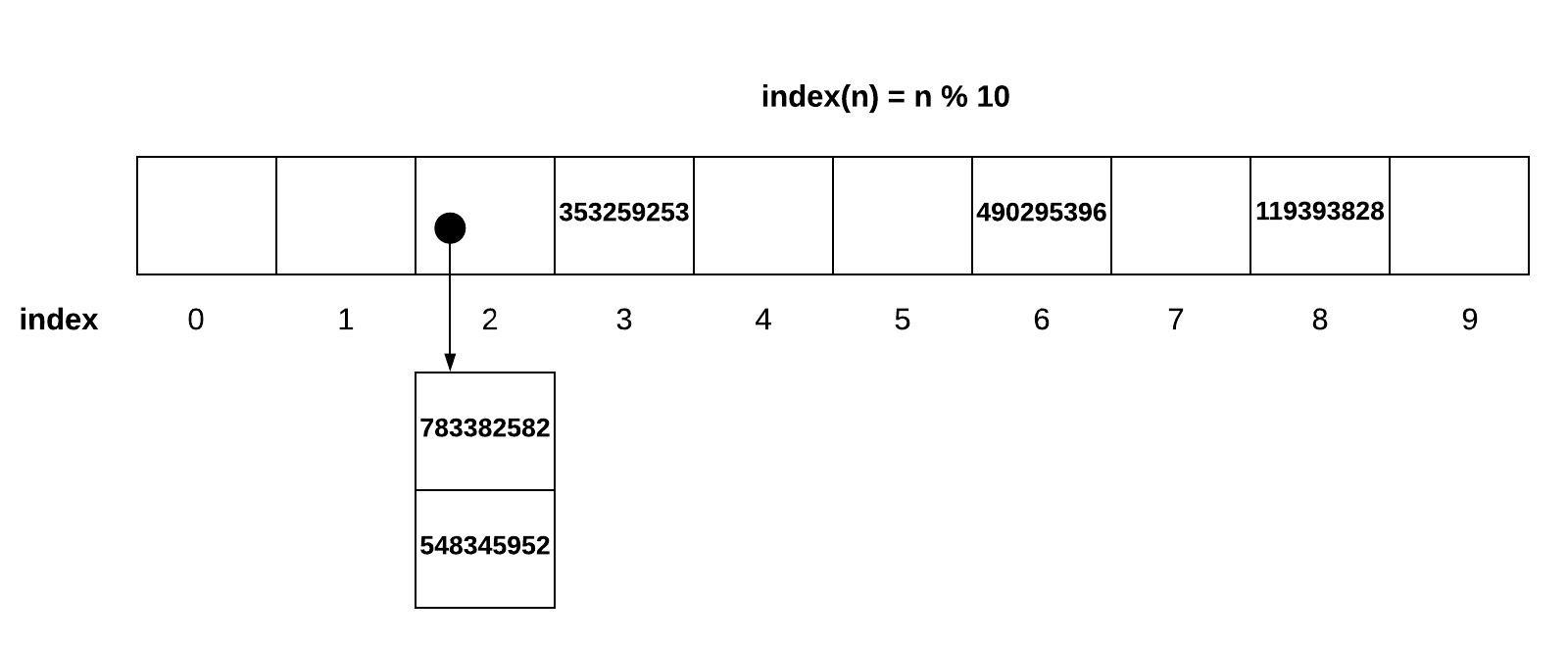
A second option is called chaining. Instead of looking for a new place for our data, we can make a list of values that occupy the same space. This does not have the adverse effect of creating clusters of conflict.
In both of these options to solve conflicts, we have an adverse effect on our O(1) performance. The use of the
index(n) hashing function is what gives us the O(1)
timing. If we have to search through several positions to find a value, or if we have to search the chained list,
we may approach O(n) if the amount of conflict is high. To avoid this, we need to increase the size of the sparse
array if the amount of conflict is too high. When we increase the size of the sparse array, then we need to
reposition all of the values by running the index(n)
function again with the increased sparse array size.
Applications with Sets
Sets have the following key characteristics:
- Fast performance for adding, removing, and finding (membership test).
- No duplicates are allowed. Most set implementations (including C#) will not give us an error when you try to add a duplicate value. This is done so that we can easily convert from a list, which may have duplicates, to a set that contains just the unique values.
- The set does not keep values in order. This occurs because the index(n) hashing function is not based on the order the value was added.
Sets have many uses, including the following:
- Finding the unique values in a list.
- Providing quick access to unique results previously calculated.
- Performing mathematical set operations such as an intersection (common values between two sets) and union (all values within two sets).
Sets in C#
In C#, the class we use to represent this kind of set that we've talked about is HashSet. The performance of each of the operations is determined based on the hashing function.
| Common Set Operation | Description | C# Code | Performance |
|---|---|---|---|
| add(value) | Adds "value" to the set | mySet.Add(value) | O(1) - Performance of hashing the value (assuming good conflict resolution) |
| remove(value) | Removes the "value" from the set | mySet.Remove(value) | O(1) - Performance of hashing the value (assuming good conflict resolution) |
| member(value) | Determines if "value" is in the set | mySet.Contains(value) | O(1) - Performance of hashing the value (assuming good conflict resolution) |
| size() | Returns the number of items in the set | mySet.Count | O(1) - Performance of returning the size of the set |
The following code demonstrates a couple of the mathematical operations (intersection, and union) that are available from methods in the class:
var set1 = new HashSet(){1,2,3,4,5};
var set2 = new HashSet(){4,5,6,7,8};
var set3 = set1.Intersect(set2).ToHashSet(); // This will result in {4, 5}
var set4 = set1.Union(set2).ToHashSet(); // This will result in {1, 2, 3, 4, 5, 6, 7, 8}
Video Discussion (Optional)
The following video is optional. It presents a brief discussion of the topic.
Activity Instructions
Complete the following short coding activity to practice using Sets.
Activity: Counting Duplicates
Open the course repository and browse to the week03/learn folder.
Implement the CountDuplicates function in the DuplicateCounter class using a set. This function
should make use of a set to help in counting duplicates.
Key Terms
- chaining
- A method of removing conflicts in a set in which all items that hash to the same index are chained together into a single data structure stored in that target index. When looking for data, the code will need to traverse the data structure.
- hashing
- The process of mapping an item to an index location using a hashing function. Since the function does not require searching through the data structure, hashing can result in an O(1) in the best case.
- hashing function
- A function that converts the value of an item to a numerical index value. The hashing function will include a modulo operation to ensure the resulting index is within range of the sparse array.
- open addressing
- A method of removing conflicts in a set in which a new empty location is found elsewhere in the sparse array. There are multiple ways of finding an empty location including moving over 1 index at a time until one is found. When looking for data, the code will need to follow this search strategy until something is found.
- set
- A data structure that maps data to an index based on a hashing function. Sets can only hold unique data because of the hashing function. Sets are useful for summarizing data and finding duplicates.
- sparse array
- An array that is only partially filled. To avoid conflicts in a set, a sparse array must have sufficient empty space to allow for new additions. If a sparse array gets too full, a large sparse array could be created with an updated hashing function.
Submission
When you have finished all of the learning activities for the week, return to Canvas and submit the associated quiz there.
Other Links:
- Return to: Week Overview | Course Home
